Andrews, Tara Lee, Katholieke Universiteit Leuven, Belgium, tara.andrews@arts.kuleuven.be Macé, Caroline, Katholieke Universiteit Leuven, Belgium, caroline.mace@arts.kuleuven.be
The construction of a stemma codicum from the manuscript witnesses to a given text remains a somewhat divisive issue in philology. To a classical philologist, it is a necessary first step toward creating a critical edition of the text;1 to a scholar who adheres to the principles of new philology, the assumptions inherent in the construction of a stemma are so fundamentally unsound that the exercise is pointless.2
The advent of digital philology demands a fresh look at the practice of stemmatology; indeed there has been a great deal of work in the past two decades on the subject, and in particular on the applicability of similar work from the field of evolutionary biology on the reconstruction of phylogenetic relationships between species.Among the numerous works on this subject are: 3 More recent work has begun to overcome the limitations of these techniques when applied to manuscript texts, such as the biological assumption that no extant species is descended from another, or the assumption that any ancestor species has precisely two descendants, or the converse assumption that any descendant species has precisely one ancestor.4
Despite this considerable methodological progress, the fundamental assumptions at the core of stemmatology have yet to be formalised, or even seriously questioned. The purpose of this paper is to revisit these assumptions and simplifications; to propose a model for the representation of texts in all their variations that is tractable to computational analysis; to set forth a method for the evaluation of stemma hypotheses with reference to text variants, and vice versa; and to discuss the means by which we can provide the field of stemmatology with a formal underpinning appropriate for the abilities that modern computational methods now provide us to handle vast quantities of data.
Modelling a text tradition
The first step to computational analysis of any text tradition is to model it programmatically. This act of object modelling is distinct from, and orthogonal to, text encoding – the component texts may reach us in a variety of forms, including TEI XML and its critical apparatus module, CSV-format alignment tables, a base text and a list of variants exported from a word processor, or even individual transcriptions that remain to be collated. All of these must be parsed into a uniform computational object model for further programmatic analysis.
Our model is relatively simple, taking into account only those features of the text that are computationally useful for our purposes. We define a tradition as the union of all the versions of a text that exist, represented by its witnesses. A collation is the heart of the tradition, representing in a unified way the entire text with all its known variations. We have adapted the variant graph model proposed by Schmidt and Colomb5 for this purpose. Whereas the Schmidt/Colomb model is a single graph, where readings are represented along edges, ours is a pair of graphs, in which readings are represented by vertices. The set of vertices is identical in both graphs; in the ‘sequence’ graph, the witnesses themselves are represented as a set of paths. Each witness path is directed and acyclic, taking a route through the reading vertices from beginning to end, according to the order of its text. The witness path may branch, if for example the text contains corrections by the original scribe(s) or by later hands; the branches are labeled appropriately. If transpositions are present, the graph as a whole is not directed and acyclic (DAG); we have therefore found it most useful to represent transposed readings as separate vertices, linked through a relationship as described below. A DAG may then be trivially transformed into an alignment table, with transpositions handled either as separate rows in the table or as variant characters within the same row.
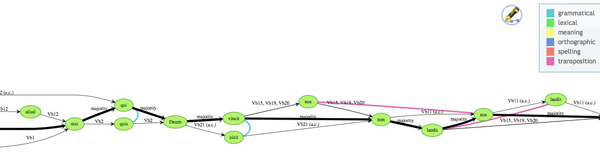 Figure 1: A portion of a variant graph, with directed witness paths and undirected relationships
Figure 1: A portion of a variant graph, with directed witness paths and undirected relationships
The second graph concerns relationships between readings, or types of variation that occur within the text. We may specify that two different readings are orthographic or syntactic variants of the same root word, or that they have some semantic relationship to each other. We may also specify transpositions in this way. The result is an unconnected and undirected graph that adds extra information to the sequence graph without compromising its properties. The relationship information allows association and regularization of reading data, producing thereby more exact versions of alignment tables for our statistical procedures.
Modelling a stemma hypothesis
The goal of our research is to arrive at an empirical model of medieval text transmission, and set forth a formalized means of deducing copying relationships between texts. As such, we have two tasks before us. We must be able to evaluate a stemma hypothesis according to the variation present in a text tradition, and we must be able to evaluate variants in a tradition according to a given stemma hypothesis.
The problem becomes computationally tractable once we realize that a stemma hypothesis is also a DAG. No matter the complexity of the stemma, no matter the degree of ‘horizontal transmission’, a stemma can be represented as a connected and rooted DAG, where each extant or hypothesized manuscript is a vertex, and each edge describes a source relationship from one manuscript to another. (In our model, any stemma has a single archetype; where multiple archetypes exist in a text tradition, we must either consider a common theoretical origin for these archetypes, or speak of multiple stemmata.)
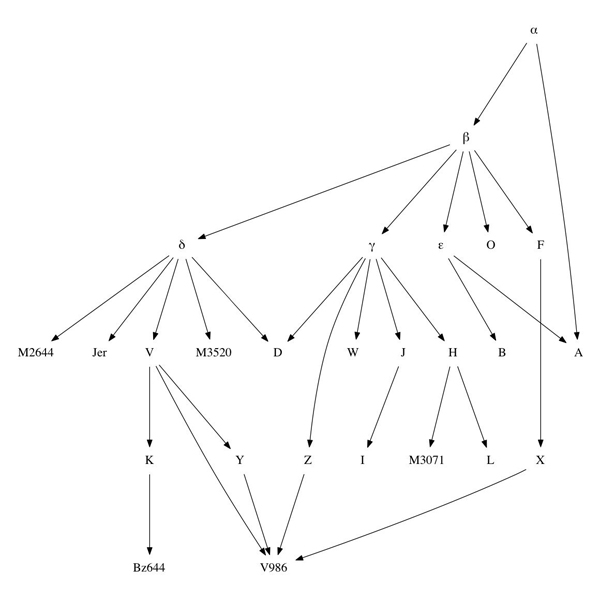 Figure 2: An arbitrarily complex stemma, represented as a DAG
Figure 2: An arbitrarily complex stemma, represented as a DAG
In cooperation with the Knowledge Representation and Reasoning group within the KU Leuven Computer Science faculty,6 we have developed a method for evaluating sets of variants against a stemma hypothesis of arbitrary complexity, testing whether any particular set of variants aligns with the stemma hypothesis, and measuring the relative stability of particular readings (defined in terms of how often they are copied vs. how often they are altered). In conjunction with the variant graphs of our text model, we are also able programmatically to draw some empirical conclusions about the relationships between readings as they are altered within the text.
An empirical approach to text variation
The idea of distinguishing ‘text-genealogical’ variants from the coincidental sort is not new;7 with the exception of U. Schmid (2004), however, none of the approaches taken have been empirical, in accordance with text relationships known from outside the variant tables. Given the means to quickly evaluate a stemma in detail according to the variants present in the text, distinguishing those variants that follow the stemma from those that do not, we should now easily be able to arrive at an empirical classification of genealogically ‘significant’ and ‘insignificant’ variants. This threatens to create a problem of circular logic: how to retrieve the genealogical variants in the real world? We build hypotheses on the basis of variation; we accept or reject variants as ‘genealogical’ based on the hypothesis. How do we break the cycle?8
We may adopt two approaches to anchor our methods in external results. First we test our methods on artificial traditions that have been created for the testing of stemmatological methods. These traditions are convenient in that the true stemmata are known, but they cannot reflect the true conditions under which medieval texts were copied. Thus we must also use ‘real’ text traditions, whose true stemmata are not fully known; in many medieval traditions, however, some paratextual information (e.g. colophon notations, physical damage or other physical characteristics of the texts) survives and can be used to establish or verify copying relationships. In our presentation we will discuss the results obtained on three artificial traditions, and three real medieval traditions with credible stemma hypotheses derived from external characteristics.
Conclusion
When examining a medieval tradition, we can rarely be certain what the scribe has copied in a text, and what has changed coincidentally or independently. To date, stemmatic reasoning has relied on the question of whether the scholar finds it likely that a given variant was preserved in copies. Given the models and methods for analysis proposed herein, we have an opportunity to remove this limitation of ‘assumed likelihood’ and take all the evidence of a text into account, to build a statistical model independent of the constraints of evolutionary biology, using statistical probability rather than scholarly instinct alone.
References
Blockeel, H., B. Bogaerts, M. Bruynooghe, B. de Cat, S. de Pooter, M. Denecker, A. Labarre, and J. Ramon (2012). Modeling Machine Learning Problems with FO(·). Submitted to the 28th International Conference on Logic Programming.
Cameron, H. D. (1987). The upside-down cladogram. Problems in manuscript affiliation. In H. M. Hoenigswald and L. F. Wiener (eds.), Biological metaphor and cladistic classification : an interdisciplinary perspective. Philadelphia: U of Pennsylvania P.
Cerquiglini, B. (1989). Éloge de la variante : histoire critique de la philologie, Paris: Éd. du Seuil.
Howe, C. J., A. C. Barbrook, M. Spencer, P. Robinson, B. Bordalejo, and L. Mooney (2001). Manuscript Evolution. Trends in Genetics 17: 147-52.
Maas, P. (1957). Textkritik. Leipzig: Teubner.
Macé, C., and P. Baret (2006). Why Phylogenetic Methods Work: The Theory of Evolution and Textual Criticism. In C. Macé, P. Baret, A. Bozzi, and L. Cignoni (eds.), The Evolution of Texts: Confronting Stemmatological and Genetical Methods. Pisa, Rome: Istituti Editoriali e Poligrafici Internazionali.
Pasquali, G. (1962). Storia della tradizione e critica del testo. Firenze: F. Le Monnier.
Reeve, M. D. (1986). Stemmatic method: ‘Qualcosa che non funziona?’ In P. F. Ganz (ed.), The role of the book in medieval culture : proceedings of the Oxford International Symposium, 26 September-1 October 1982. Turnhout: Brepols.
Roos, T., and Y. Zou (2011). Analysis of Textual Variation by Latent Tree Structures. IEEE International Conference on Data Mining, 2011 Vancouver.
Salemans, B. J. P. (2000). Building Stemmas with the Computer in a Cladistic, Neo-Lachmannian, Way: The Case of Fourteen Text Versions of Lanseloet van Denemerken. Ph.D., Katholieke Universiteit Nijmegen.
Schmid, U. (2004). Genealogy by chance! On the significance of accidental variation (parallelisms). In P. T. van Reenen, A. den Hollander, and M. van Mulken (eds.), Studies in Stemmatology II. Amsterdam: Benjamins.
Schmidt, D., and R. Colomb (2009). A data structure for representing multi-version texts online. International Journal of Human-Computer Studies 67: 497-514.
Spencer, M., and C. J. Howe (2001). Estimating distances between manuscripts based on copying errors. Literary and Linguistic Computing 16: 467-484.
P. T. van Reenen, A. den Hollander, and M. van Mulken, eds. (2004). Studies in Stemmatology I., Amsterdam: Benjamins.
West, M. L. (1973). Textual Criticism and Editorial Technique: Applicable to Greek and Latin Texts. Stuttgart: Teubner.
Notes
1.Maas 1957; Pasquali 1962; West 1973.
2. See, among many references on this question Cerquiglini 1989; Reeve 1986.
3.Cameron 1987; Howe et al. 2001; Macé & Baret 2006; Spencer & Howe 2001.
4.Roos & Zou 2011.
5.Schmidt & Colomb 2009.
6.Blockeel et al. 2012.
7.Salemans 2000. See also papers by Wachtel, van Mulken, Schmid, Smelik, Schøsler, and Spencer et al in van Reenen et al. 2004.
8.See the critique of concerning the work of Salemans.

