| Critical Values of the Chi-Square Distribution | ||
|---|---|---|
| Degrees of Freedom | 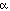 = 0.05 = 0.05 | 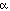 = 0.001 = 0.001
|
| 1 | 3.841 | 10.827 |
| 2 | 5.991 | 13.815 |
| 3 | 7.815 | 16.266 |
| 4 | 9.488 | 18.466 |
| 5 | 11.070 | 20.515 |
| 6 | 12.592 | 22.457 |
| 7 | 14.067 | 24.321 |
| 8 | 15.507 | 26.124 |
| 9 | 16.919 | 27.877 |
| 10 | 18.307 | 29.588 |
| Rank | Weight | X if dry | Rank | Weight | X if dry | |
| 1 | 11 | |||||
| 2 | 12 | |||||
| 3 | 13 | |||||
| 4 | 14 | |||||
| 5 | 15 | |||||
| 6 | 16 | |||||
| 7 | 17 | |||||
| 8 | 18 | |||||
| 9 | 19 | |||||
| 10 | 20 |
Rank Sum for Dry Seeds __________
Add up all the ranks for wet seeds:
Rank Sum for Wet Seeds __________
If there were no difference between the sub-samples, these rank sums would be identical! Since they are not identical, are they different enough to reject the hypothesis of equality?
The Wilcoxon or W-statistic is the lesser of the two rank sums.
This statistic is compared with a table value for 0.05 error found below. Use the two sample sizes (n1 and n2) for rows and columns to locate the table value.
What is the table value? ___________
| n2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| n1 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | - | - | - | - | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 |
| 3 | - | - | 6 | 6 | 7 | 8 | 8 | 9 | 10 | 10 | 11 | 11 | 12 | 13 | 13 | 14 | 15 | 15 | 16 | 17 | 17 | 18 | 19 | 19 | 20 |
| 4 | - | - | - | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| 5 | - | - | - | - | 19 | 20 | 21 | 23 | 24 | 26 | 27 | 28 | 30 | 31 | 33 | 34 | 35 | 37 | 38 | 40 | 41 | 43 | 44 | 45 | 47 |
| 6 | - | - | - | - | - | 28 | 29 | 31 | 33 | 35 | 37 | 38 | 40 | 42 | 44 | 46 | 47 | 49 | 51 | 53 | 55 | 57 | 58 | 60 | 62 |
| 7 | - | - | - | - | - | - | 39 | 41 | 43 | 45 | 47 | 49 | 52 | 54 | 56 | 58 | 61 | 63 | 65 | 67 | 69 | 72 | 74 | 76 | 78 |
| 8 | - | - | - | - | - | - | - | 51 | 54 | 56 | 59 | 62 | 64 | 67 | 69 | 72 | 75 | 77 | 80 | 83 | 85 | 88 | 90 | 93 | 96 |
| 9 | - | - | - | - | - | - | - | - | 66 | 69 | 72 | 75 | 78 | 81 | 84 | 87 | 90 | 93 | 96 | 99 | 102 | 105 | 108 | 111 | 114 |
| 10 | - | - | - | - | - | - | - | - | - | 82 | 86 | 89 | 92 | 96 | 99 | 103 | 106 | 110 | 113 | 117 | 120 | 123 | 127 | 130 | 134 |
| 11 | - | - | - | - | - | - | - | - | - | - | 100 | 104 | 108 | 112 | 116 | 120 | 123 | 127 | 131 | 135 | 139 | 143 | 147 | 151 | 155 |
| 12 | - | - | - | - | - | - | - | - | - | - | - | 120 | 125 | 129 | 133 | 138 | 142 | 146 | 150 | 155 | 159 | 163 | 168 | 172 | 176 |
| 13 | - | - | - | - | - | - | - | - | - | - | - | - | 142 | 147 | 152 | 156 | 161 | 166 | 171 | 175 | 180 | 185 | 189 | 194 | 199 |
| 14 | - | - | - | - | - | - | - | - | - | - | - | - | - | 166 | 171 | 176 | 182 | 187 | 192 | 197 | 202 | 207 | 212 | 218 | 223 |
| 15 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 192 | 197 | 203 | 208 | 214 | 220 | 225 | 231 | 236 | 242 | 248 |
| 16 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 219 | 225 | 231 | 237 | 243 | 249 | 255 | 261 | 267 | 273 |
| 17 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 249 | 255 | 262 | 268 | 274 | 281 | 287 | 294 | 30 |
| 18 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 280 | 287 | 294 | 301 | 307 | 314 | 321 | 328 |
| 19 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 313 | 320 | 328 | 335 | 342 | 350 | 357 |
| 20 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 348 | 356 | 364 | 371 | 379 | 387 |
| 21 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 385 | 393 | 401 | 410 | 418 |
| 22 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 424 | 432 | 441 | 450 |
| 23 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 465 | 474 | 483 |
| 24 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 507 | 517 |
| 25 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 552 |
Decision Rule:
We reject the hypothesis of equality if the W-statistic is equal to or less than the table value.
Decision:
Based on the Wilcoxon Rank-Sum test, the hypothesis:
"Soaking causes beans to expand" is: rejected not rejected
Our hypothesis used the term "expand" and our prediction used the term "larger." In our experiment we tested the weight of the soaked beans.
What weight adjective would describe the soaked beans? __________________________
Observation: Our soaked beans sure do seem larger than the dry beans, but how can we measure the volume of an oddly shaped living-bean?
Question: Does soaking beans cause them to expand?
Hypothesis: Soaking does not cause beans to expand. [note alternate!]
Prediction: If soaking does not cause beans to expand, beans which are soaked will not be significantly larger than dry beans.
Experiment: Measure the volume of bean seeds by displacement of water in a graduated cylinder. Calculate the volume per bean by dividing the total volume of beans added by the number of beans added.
| Soaked Beans | Dry Beans | |
|---|---|---|
| Final Liquid Level | mL | mL |
| Starting Level | 14 mL | 14 mL |
| Total Volume of Beans Added | mL | mL |
| Number of Beans Added | beans | beans |
| Volume per Bean | mL/bean | mL/bean |
The group of dry beans receiving no treatment is the ________________ group.
The group of soaked beans is called the ________________ group.
Analysis:
Examining the volume per bean, there is a striking difference.
Can we perform a T-test or a Wilcoxon test on these data? Yes No
If No, why not?__________________________________________________
If we wanted to redo our volume measurements, how could we do them so that we could use a statistical test for our analysis?
______________________________________________________________
We will not make any further measurements, but perhaps we may satisfy our need for significance by recalling that scientists find 5% error acceptable.
Calculate the ratio of the volume per soaked bean to the volume per dry bean._________
The soaked beans occupy ________% of the volume of the dry beans.
Is there at least a 5% difference between the beans? Yes No
Decision:
Based on a displacement test, the hypothesis:
"Soaking does not cause beans to expand" is: rejected not rejected
Why did we choose to rewrite our hypothesis this time to its alternate "no effect" form?
___________________________________________________________
___________________________________________________________
By having our hypotheses rejected, are we poor scientists? Yes No
Why did we not have the option to "prove" any of our hypotheses?________________________
I'm sure you have seen a coin toss at the beginning of a sporting event. A coin flips over and over in the air and lands on one side. One side is called "heads" (because that side has a face on it) and the other side is called "tails" (because that side is opposite the face). You might guess that it is equally likely that the coin lands "heads" up as it is to land "heads" down. In other words, if you tossed the coin 20 times you would expect "heads" to come up about 10 of those times. That should be true of a "balanced" coin. Of course it might be possible to make an unbalanced coin that would allow some cheating. An unbalanced coin would come up "heads" more than 10 out of 20 tosses (or perhaps less than 10/20 tosses).
You are presented with two coins. The idea is to test whether they are balanced.
Question:____________________________________________________________________
Hypothesis:__________________________________________________________________
Prediction:___________________________________________________________________
Experiment:
Put the outcomes of 20 tosses for each coin in the separate charts below.
Mark H for "heads" and T for "tails".
| Single coin | Hybrid coin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Single Coin | Hybrid Coin | ||||
|---|---|---|---|---|---|
| Heads | Tails | Heads | Tails | ||
| Observed | |||||
| Expected | |||||
| Observed-Expected | |||||
| (Observed-Expected)2 | |||||
| (Observed-Expected)2 Expected | |||||
| X2 Stat = Sum (Observed-Expected)2 Expected | |||||
| Degrees of Freedom = n-1 | |||||
| X2 Table Value | |||||
| Decision | |||||
Decision Rule: If X2 Stat is greater than or equal to X2 Table Value, then reject model.
Conclusion:___________________________________________________________
Question:____________________________________________________________
Hypothesis:__________________________________________________________
Prediction:___________________________________________________________
Experiment: Put the outcomes of 24 tosses for each die. Mark outcomes as 1, 2, 3, 4, 5, or 6.
| Black die with White spots | Black die with Silver spots | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Analysis: Perform X2 tests in the tables below:
| Black die with White spots: | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Observed | ||||||
| Expected | ||||||
| Observed-Expected | ||||||
| (Observed-Expected)2 | ||||||
| (Observed-Expected)2 Expected | ||||||
| X2 Stat = Sum (Observed-Expected)2 Expected | ||||||
| Degrees of Freedom = n-1 | ||||||
| X2 Table Value | ||||||
| Decision |
| Black die with Silver spots: | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Observed | ||||||
| Expected | ||||||
| Observed-Expected | ||||||
| (Observed-Expected)2 | ||||||
| (Observed-Expected)2 Expected | ||||||
| X2 Stat = Sum (Observed-Expected)2 Expected | ||||||
| Degrees of Freedom = n-1 | ||||||
| X2 Table Value | ||||||
| Decision |
Conclusion:__________________________________________________________
There is more to statistics in plant physiology than just comparison of means (t-test and Wilcoxon) and discrete ratios of outcomes (Chi-squared), but this is a start. Later in the semester we will do a regression test...that is an important one for dose-dependent responses (for example).
| Critical Values of the Chi-Square Distribution | ||
|---|---|---|
| Degrees of Freedom | 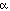 = 0.05 = 0.05 | 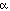 = 0.001 = 0.001
|
| 1 | 3.841 | 10.827 |
| 2 | 5.991 | 13.815 |
| 3 | 7.815 | 16.266 |
| 4 | 9.488 | 18.466 |
| 5 | 11.070 | 20.515 |
| 6 | 12.592 | 22.457 |
| 7 | 14.067 | 24.321 |
| 8 | 15.507 | 26.124 |
| 9 | 16.919 | 27.877 |
| 10 | 18.307 | 29.588 |
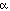 . The probability is less than a pre-selected critical value. Please note that this does NOT mean the result is important or interesting (scientifically significant).
. The probability is less than a pre-selected critical value. Please note that this does NOT mean the result is important or interesting (scientifically significant).
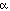 = 0.05; both are statistically significant. Many plant physiology articles will show numbers in tables with superscript symbols as found in the key below:
= 0.05; both are statistically significant. Many plant physiology articles will show numbers in tables with superscript symbols as found in the key below:
| symbol | p | meaning |
|---|---|---|
| ns | >0.05 | not significant |
| * | <0.05 | significant |
| ** | <0.01 | very significant |
| *** | <0.001 | extremely significant |
Type I error: rejecting a true null hypothesis (convicting the innocent)If you set
Type II error: not rejecting a false null hypothesis (failing to convict the guilty)
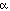 (reasonable doubt) to a very low value, your test makes very few Type I errors but makes many Type II errors. If you set
(reasonable doubt) to a very low value, your test makes very few Type I errors but makes many Type II errors. If you set 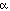 to a very high value, your test makes many Type I errors but very few Type II errors. Obviously some compromise value is needed; convention selects
to a very high value, your test makes many Type I errors but very few Type II errors. Obviously some compromise value is needed; convention selects 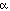 = 0.05. Conclusion: it is OK to show p values to your audience, but don't use the interpretations under the word meaning in the table above.
= 0.05. Conclusion: it is OK to show p values to your audience, but don't use the interpretations under the word meaning in the table above.
There are situations when you want to minimize one of the two types of errors and thus would choose a critical value other than 0.05...
You are screening possible new pesticides to control a fungal pathogen of corn plants. The screening tests are rather inexpensive and fast, so you don't care how many type I errors you make (pesticide is ineffective but you will keep testing it). What you really want to avoid is a type II error (pesticide is effective but you stop testing it). You want to use a critical value of 0.2 or 0.1. (In final testing of pesticide for "incurable" disease, you would need to go the other direction!!)
Go back to the Course Schedule.