Original URL: http://www.cogs.susx.ac.uk/users/gabro/lsys/lsys.html
Central to L-systems, is the notion of rewriting, where the basic idea is to define complex objects by successively replacing parts of a simple object using a set of rewriting rules or productions. The rewriting can be carried out recursively.
The most extensively studied and the best understood rewriting systems operate on character strings. Chomsky's work on formal grammars (1957) spawned a wide interest in rewriting systems. Subsequently, a period of fascination with syntax, grammars and their application in computer science began, giving birth to the field of formal languages.
Aristid Lindenmayer's work introduced a new type of string rewriting mechanism, subsequently termed L-systems. The essential difference between Chomsky grammars and L-systems lies in the method of applying productions. In Chomsky grammars productions are applied sequentially, whereas in L-systems they are applied in parallel, replacing simultaneously all letters in a given word. This difference reflects the biological motivation of L-systems. Productions are intended to capture cell divisions in multicellular organisms, where many division may occur at the same time.
Lets us consider strings built of two letters a and b (they may occur many times in a string). For each letter we specify a rewriting rule. The rule a -> ab means that the letter a is to be replaced by the string ab, and the rule b -> a means that the letter b is to be replaced by a. The rewriting process starts from a distinguished string called the axiom. Let us assume that it consist of a single letter b. In the first derivation step (the first step of rewriting) the axiom b is replaced by a using production b -> a. In the second step a is replaced by ab using the production a -> ab. The word ab consist of two letters, both of which are simultaneously replaced in the next derivation step. Thus, ais replaced by ab , b is replaced by a, and the string aba results. In a similar way (by the simultaneous replacement of all letters), the string aba yields abaab which in turn yields abaababa, then abaababaabaab, and so on.
b | a _|_ a b _| \ a b a _| | |_ a b a a b _/ | |_ |_ \ a b a a b a b aFormal definitions of D0L-systems and their operation can be found in (Prusinkiewicz and Hanan 1989; Prusinkiewicz and Lindenmayer 1991)
Many fractals (or at least their finite approximations) can be thought of as sequences of primitive elements -line segments. To produce fractals, strings generated by L-systems must contain the necessary information about figure geometry. A graphic interpretation of strings, based on turtle geometry, is described by Prusinkiewicz et al. (1989), (1990). This interpretation may be used to produce fractal images.
A state of the turtle is defined as a triplet (x, y, a), where the Cartesian coordinates (x, y) represent the turtle's position, and the angle a, called the heading, is interpreted as the direction in which the turtle is facing. Given the step size d and the angle increment b, the turtle can respond to the commands represented by the following symbols:
F Move forward a step of length d. The state of the turtle changes to (x',y',a), where x'= x + d cos(a) and y'= y + d sin(a). A li- ne segment between points (x,y) and (x',y') is drawn. f Move forward a step of length d without drawing a line. The state of the turtle changes as above. + Turn left by angle b. The next state of the turtle is (x,y,a+b). - Turn left by angle b. The next state of the turtle is (x, y,a-b).All other symbols are ignored by the turtle (the turtle preserves its current state).
Given a string v, the initial state of the turtle (x0,y0,a0), and fixed parameters d and b, the turtle interpretation of v is the figure (set of lines) drawn by the turtle in response to the string v.
The above description gives us a rigorous method for mapping strings to pictures, which may be applied to interpret strings generated by L-systems. Next figure shows four approximations of the curve known as ``quadratic Koch island''. These figures were obtained by interpreting strings generated by the following L-system:
w: F+F+F+F p: F -> F+F-F-FF+F+F-F


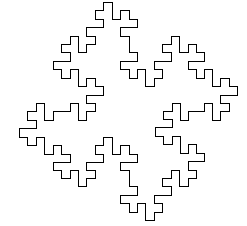

The images correspond to the strings obtained by derivations of length n = 0, 1, 2 and 3 respectively. The angle increment b is equal to 90 degrees.
In his work, Lindenmayer, introduced a notation for representing graph-theoretic trees using strings with brackets. The idea was to formally describe branching structures found in many plants, from algae to trees, using the framework of L-systems. Again, posterior geometric interpretations of strings with brackets were proposed for realistic modelling of plants. Thus, to represent branching structures, L-systems alphabet is extended with two new symbols, `[' and `]', to delimit a branch. They are interpreted by the turtle as follows:
[ Pop a state from the stack and make it the current state of the turtle. ] Push the current state of the turtle onto a pushdown stack.An example of a bracketed string and its turtle interpretation, obtained in derivations of length n = 1 - 5, are shown in the next figure . These figures were obtained by interpreting strings generated by the L-system:
w: F p: F -> F[-F]F[+F][F]
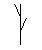
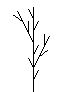



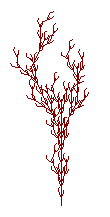




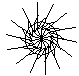
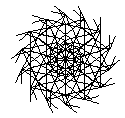
Visually appealing figures not resembling plants, were also obtained using a Genetic Algorithm with a fitness function favouring bilateral symmetric structures.

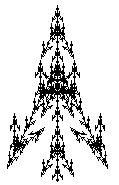
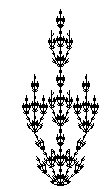
Gabriela Ochoa, gabro@cogs.susx.ac.uk (12/02/98)